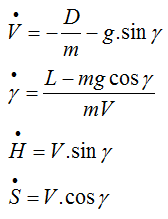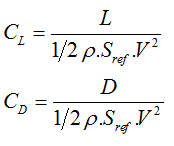Let's start preparing software platform for building our dummy flight simulator:
- Python is a very powerful and clear programming language. If you have programmed before, you'll have no problem for understanding python codes;
- SciPy is Python library for scientific programming. It is necessary download NumPy and, actual, SciPy;
- PyGame "is a set of Python modules designed for writing games".
Designing code
Using Python, which has a different purpose than pure scientific tools as Scilab, we got more flexibility to modularize code and to make it become more reusable for future improvements.
So we are going to design our simulator with object oriented programming (OOP). If you are not familiar with this paradigm, we are going to give a very simple explanation that will hopefully become more clear with the codes written later.
OOP can be understood as a way to crack your code in little modules called classes, which are recipes for keeping together a set of data and a set of functions that change these data. Semantically, when modeling a problem, we bound the entities of the problem in classes, giving to them attributes and methods, i.e. actions that can change the entities behavior.
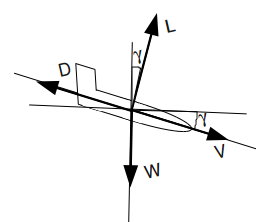
OK! Let's stop being abstract. See our physics model for gliding. We can identify an entity for Atmosphere stuff. So we can create the class Atmosphere with attributes about the values of temperature and density, for example; and with methods for changing temperature and density according height. Another class could be Aircraft with attributes like position and velocity, and methods to increase or decrease CL (this would be equivalent to give control to make aircraft to go up or to go down).
We call object, an individual of a given class. In other words, class is a recipe to build an object. For example, since we have an Aircraft class, we could create two different objects depending on values of their attributes, different polar drag, for instance.
Our model will contain the following main classes: Atmosphere, Aircraft and Flight.
Atmosphere class
For simplicity we're going to put all our code in just one python module (.py file extension). So, choose your favorite text editor and start putting the following code:
#!/usr/bin/python
# -*- coding: utf-8 -*-
from math import exp
class Atmosphere(object):
T0 = 288.15
H0 = 0
g0 = 9.80665
L = -6.5e-3
R = 287.05287
rho0 = 1.225
def temperature(self,H):
T = self.T0
if H<=11000:
T = self.T0 + self.L*(H-self.H0)
else:
T = self.temperature(11000)
return T
def density(self,H):
rho = self.rho0
if H<=11000:
rho = self.rho0*(self.temperature(H)/self.T0)\
**(-(1+self.g0/(self.R*self.L)))
else:
rho = self.density(11000)*exp(-self.g0*\
(H-11000)/(self.R*self.temperature(11000)))
return rhoTwo initial lines are just some conventions and they can be even neglected for our purposes. Then we import exponential function (exp) from math library. Finally, we start code Atmosphere class. See that this code is very similar to Scilab code, but this time we have unified all atmospheric stuff in just one code structure, the class. Realize that methods are declared with def keyword and for accessing attribute values we have to use self identifier.
To test the code you can save the module as gliding.py and call it by command line:
$ python -i gliding.py
>>> a = Atmosphere()
>>> a.density(600)
1.1559768882668726
>>> a.temperature(600)
284.25In this test you are creating an object a from Atmosphere class and calling its methods density and, after, temperature for calculating these measures at height 600m.
Aircraft class
Now, the entity Aircraft. We should put CL and CD as methods, receiving angle of attack as parameter, but for our gliding flight we're going to consider constant CL or to change it directly. In other words, in real aircrafts, pilot got control over aerodynamic surfaces to change angle of attack. That changes CL. Here, we're going to make user (pilot) change CL value, directly, i.e. CL will be our control. To make it, we put an attribute CL_constant. Below it is the code you can append to previous code.
import math
class Aircraft(object):
CD0 = 0
taper_ratio = 0
aspect_ratio = 0
wing_area = 0
mass = 0
k = 0
CL_constant = 1.0
def __init__(self, CD0, taper_ratio, aspect_ratio, wing_area, mass):
self.CD0 = CD0
self.taper_ratio = taper_ratio
self.aspect_ratio = aspect_ratio
self.wing_area = wing_area
self.mass = mass
self.k = 1/(math.pi*aspect_ratio*taper_ratio);
def CD(self,alfa=0.0):
return self.CD0+self.k*self.CL(alfa)**2
def CL(self,alfa=0.0):
return self.CL_constantTesting the code in python interpreter:
$ python -i gliding.py
>>> a = Aircraft(CD0=0.0115, taper_ratio=0.94, \
aspect_ratio=17, wing_area=16.01, mass=512)
>>> a.CL()
1.0
>>> a.CD()
0.031419266970199665
>>> a.CL_constant = 1.5
>>> a.CL()
1.5
>>> a.CD()
0.056318350682949242Flight class
This class uses some more specific object concepts as inheritance and composition. One class can inherits behavior from another class so that this subclass got the same methods of your superclass and, possibly, further methods. In our case, we have created a big class called Flight which can be reusable for many different kind of flights with different differential equation systems (ODES) modeling it. In Python you specify superclass for your class in parentheses following class name in class declaration. All previous classes inherits from object class (here you can see the reason for that). FlightSail class below inherits from Flight.
Flight class got methods for solving ODES, using SciPy library. We solve ODES by time slicing (says 1 second slice) and store ODES solution in a vector called state_history containing tuples in the form (t,y) where y is the vector representing one state of flight. In gliding flight y contains velocity, height, range, etc. Below we can see both classes Flight and subclass FlightSail.
import math
from scipy.integrate import ode
from scipy.integrate import odeint
from scipy.optimize import fsolve
class Flight(object):
"""Subclass this class and implement mech_ode_sys method
"""
aircraft = None
atmosphere = None
def __init__(self,aircraft,atmosphere):
self.aircraft = aircraft
self.atmosphere = atmosphere
def mech_ode_sys(self, t, state):
"""Must be implemented by subclass
"""
def start(self, initial_state, t_0 = 0, dt = 1):
self.ode_solver = ode(self.mech_ode_sys).set_integrator('vode')
self.ode_solver.set_initial_value(initial_state, t_0)
self.dt = dt
self.state_history = [[0.0,initial_state]]
def next_state(self):
if self.ode_solver.successful():
self.ode_solver.integrate(self.ode_solver.t+self.dt)
self.state_history.append((self.ode_solver.t, self.ode_solver.y,))
return [self.ode_solver.t, self.ode_solver.y]
else:
return None
def solve(self,t):
"""Solve ODE system for a given array of values t
"""
def func(state,t):
return self.mech_ode_sys(t, state)
y0 = self.state_history[-1][1]
y = odeint(func,y0,t)
states = zip(t,y[:])
self.state_history += states
return states
class FlightSail(Flight):
VELOCITY = 0
GAMMA = 1
HEIGHT = 2
RANGE = 3
def __init__(self,aircraft,atmosphere):
super(FlightSail,self).__init__(aircraft,atmosphere)
def mech_ode_sys(self, t, state):
"""state is a tuple in the form (Velocity,gamma,Height,Range)
"""
V = state[VELOCITY]
gamma = state[GAMMA]
H = state[HEIGHT]
R = state[RANGE]
CL = self.aircraft.CL()
CD = self.aircraft.CD()
m = self.aircraft.mass
rho = self.atmosphere.rho(H)
A = self.aircraft.wing_area
L = 0.5*rho*V**2*A*CL
D = 0.5*rho*V**2*A*CD
V_p = (-D-m*self.atmosphere.g_0*math.sin(gamma))/m
gamma_p = (L-m*self.atmosphere.g_0*math.cos(gamma))/(m*V)
H_p = V*math.sin(gamma)
R_p = V*math.cos(gamma)
return [V_p, gamma_p, H_p, R_p]Putting it all together
Now, instantiating the same problem from previous post.
import math
atmosphere = Atmosphere()
a = Aircraft(CD0=0.0115, taper_ratio=0.94, \
aspect_ratio=17, wing_area=16.01, mass=512)
a.CL_constant = 0.75
sail = FlightSail(aircraft=a, atmosphere=atmosphere)
V_0 = 30
gamma_0 = -3*math.pi/180
H_0 = 600
R_0 = 0
state_0 = (V_0, gamma_0, H_0, R_0)
sail.start(initial_state=state_0)
aircraft_state = list(state_0)
MAX_RANGE = 14000For using PyGame we have put a profile aircraft figure (in our case Super Tucano) and just update its position in a 640 x 480 screen, let CL ranging according up and down keys, and adjusting path angle, rotating the figure (this is not correct, but we are neglecting angle of attack here). PyGame code is shown below:
pygame.init()
SCREEN_X_MAX = 640
SCREEN_Y_MAX = 480
screen = pygame.display.set_mode((SCREEN_X_MAX,SCREEN_Y_MAX))
tucano_img_original = pygame.image.\
load('supertucano_lateral_menor.bmp').convert()
pygame.display.update()
tucano_img = None
clock = pygame.time.Clock()
clock.tick(10)
start = False
while True:
for event in pygame.event.get():
if event.type == pygame.QUIT:
sys.exit()
elif event.type == pygame.KEYDOWN:
start = True
key = pygame.key.get_pressed()
if key[pygame.K_UP]:
sail.aircraft.CL_constant += 0.1
print "CL increasing to: "+str(sail.aircraft.CL_constant)
elif key[pygame.K_DOWN]:
sail.aircraft.CL_constant -= 0.1
print "CL decreasing to: "+str(sail.aircraft.CL_constant)
if start:
state = sail.next_state()
#print state
pygame.display.set_caption('Sail Flight t = '+str(state[0]))
aircraft_state = [i for i in state[1]]
x = aircraft_state[FlightSail.RANGE]/float(MAX_RANGE)\
*SCREEN_X_MAX
y = SCREEN_Y_MAX - float(aircraft_state[FlightSail.HEIGHT])\
/H_0*SCREEN_Y_MAX
tucano_img = pygame.transform.rotate(tucano_img_original,\
aircraft_state[FlightSail.GAMMA]/math.pi*180)
screen.fill((255,255,255))
screen.blit(tucano_img,(x,y))
pygame.display.update()
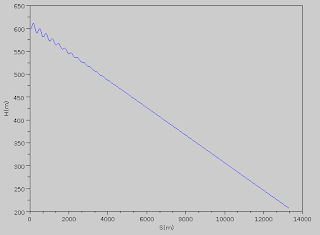
pygame.time.delay(100)Figure below shows whole code running (using python gliding.py at command line).

And that is it! Keys UP and DOWN changes CL directly, what is not quiet representative but it is fun though.